The Secret Life of Extension Cords
During our last session, we explored the water-flow/electric-current-flow analogy and summed it up in a few sentences that are worth repeating:
• Water: The pressure created by the pump forces water to flow through the pipes and valves, overcoming the friction losses of the system. Higher pressure provides for more gallons per minute.
• Electricity: The voltage created by the battery forces electrons to flow through the wires and switches, overcoming the ohmic resistance of the circuit. Higher voltage provides for more amperes. (The short version of that is, “Volts push amps through ohms.”)
To be truly useful to us, we must know something about the way these three basic units relate to one another.
SORTING THE RELATIONSHIPS
Bear with me for a moment while I get some textbook/background stuff out of the way, after which I will provide you with some handy charts that will guide you to a better understanding of these things.
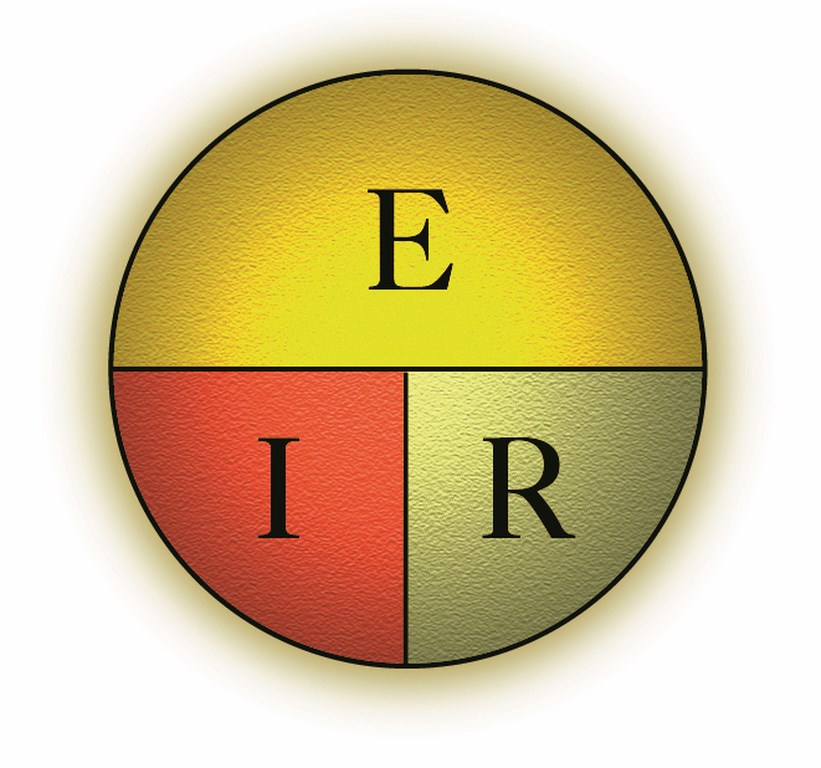
The interrelationships among these standard units – volts, amps and ohms — were investigated by Georg Simon Ohm during the 1820s. He determined that the current flow produced in a circuit by the application of a given voltage depended upon the resistance of the circuit. This resulted in Ohm’s Law, which is usually expressed as the equation resistance equals voltage divided by amperes.
Traditionally, physicists symbolize voltage with an E (for “electromotive force”), amperes with an I (for current “intensity”) and resistance with an R. Thus, Ohm’s Law is often shown as R = E/I.
The rules of mathematics allow us to express that equation in two other forms: I = E/R or E = IR. From this we see that whenever we know the value of any two of the units, we can calculate the value of the third unit by simple multiplication or division.
The pie chart just below is a handy aid to keeping these equations sorted out. To use it, place a finger on the unit for which you want to find a value and read the formula from the remaining two elements.
For example, if you wish to know the volts of a circuit, cover the “E” and “IR” remains, indicating that you must multiply the amperes times the resistance to find the volts. Or cover the “I” and “E over R” remains, directing you to divide the volts by the ohms to find the amperes. Likewise, cover the “R” and “E over I” remains, telling you to divide the volts by the amperes to find the ohms.
A MORE PRACTICAL TOOL
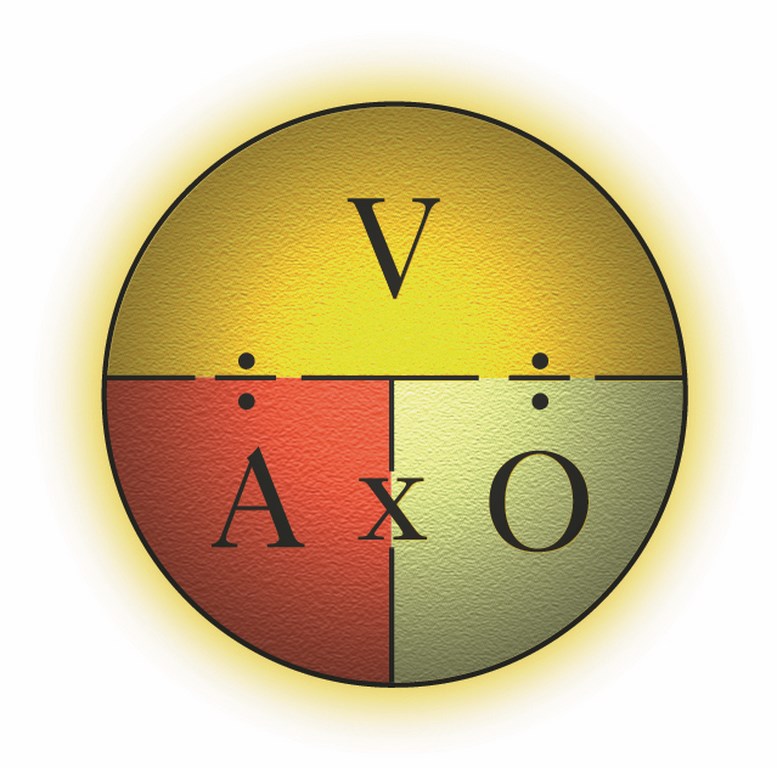
That’s all well and good, but I believe that it is asking too much to expect people who don’t work with things electric every day to remember that “E” is volts, “I” is amperes and “R” is ohms. So let’s make a simple change to the chart to get rid of the mumbo-jumbo.
With this new chart (at right), when you put a finger on the “V,” you now clearly see “A x O.” Covering the “O” will leave “V ÷ A,” while covering the “A” shows “V ÷ O.” With this change, I believe we have a better chance of keeping these things straight when we see A, V and O representing amps, volts and ohms, respectively, than we did when they were labeled with E, I and R.
Once you become comfortable with these relationships, you will begin to find practical applications for them in dealing with all sorts of electric circuits.
For instance, although many people are aware that they should not string together several extension cords, they may have no understanding as to why it is considered bad practice. Aside from the obvious tripping hazard that might be created, there is a significant electrical consideration.
To illustrate, let’s say you want to operate a 120-volt circular saw, drawing 12 amps, at a distance of 150 feet from a wall receptacle. To span that gap, you have six 25-foot-long, 18-gauge, lightweight extension cords plugged end to end. The total resistance of those cords will be about 1.9 ohms.
How much voltage loss will take place in those cords? Try V = A x O: That’s 12 x 1.9 = 22.8. On a 120-volt circuit, you’re losing 22.8 volts – and it’s unlikely your saw will be happy operating at 97.2 volts. In fact, it will become angry and hot.
You could trade in those skimpy extension cords for three decent, medium-duty, 50 footers with 14-gauge conductors. The resistance will drop to about 0.7 ohms, so the voltage available at the saw will be approximately 112 volts. Much better. The saw’s anger subsides.
WHAT ABOUT WATT?
As handy as these pie charts are for helping us with Ohm’s Law, they do not provide us with any information on the fourth electrical unit of interest: the watt.
The watt is a bit of an oddball in this scheme of things: It is not specifically an electrical term, like volt or ampere or ohm; rather, it is the name given to the standard unit of power.
Power is defined as the rate at which work is performed or at which energy is expended. The source of the energy doesn’t matter, nor does the type of energy: We can measure it in watts. We measure the light energy of a light bulb in watts, for example. We use watts to measure the sound energy of a stereo system and the heat energy of an oven. We could just as easily rate the size of all the motors we use (and our automobile engines) in watts as well, but convention is this country long ago opted for horsepower – and we won’t give it up.
(Incidentally, the relationship between the watt and the horsepower is an interesting story in itself – one I look forward to exploring in an upcoming issue of WaterShapes.)
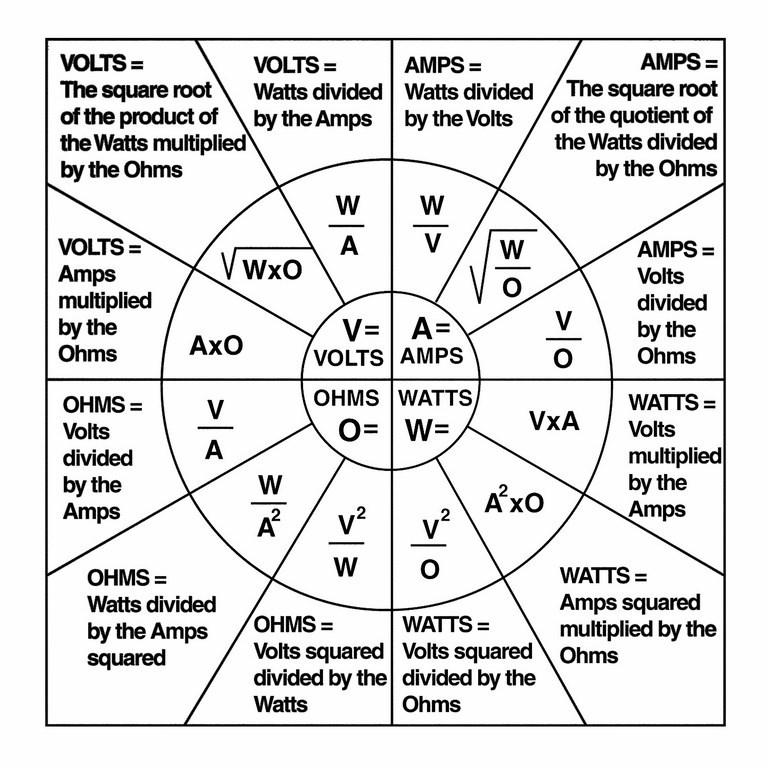
As odd as the watt is, we are fortunate that it has strong mathematical links to the other terms we are dealing with, because it allows us to expand the pie charts shown on page 68 in all sorts of helpful ways.
As you see, I have now embellished the chart shown just above to include words that talk you through each of 12 equations that should be part of your electrical vocabulary. I sincerely hope it finds a place on your wall. I think it would make a great refrigerator magnet!
Jim McNicol was a technical consultant to the swimming pool, jetted bath and spa industries. He worked on development of equipment standards for pools and spas throughout his career and was honored for his service by the National Spa & Pool Institute.