Balanced Force

Working successfully with hydraulic systems requires two things: Understanding the definitions of the basic factors involved in hydraulic calculations and seeing how those values relate to and influence each other in the real world.
The last installment in this series of articles focused on the relationship between flow and velocity with respect to water. The related concept we’ll explore this time takes our understanding of that key relationship a step farther by exploring a specific pair of additional relations summarized by two statements:
* The smaller the flow section of a pipe, the faster the velocity of the water
* The larger the flow section of the pipe, the slower the velocity of the water.
If we grasp the full meaning of those two, related concepts, we take the first step toward understanding basic fluid mechanics as it pertains to hydraulic design for custom watershapes. The last article approached this subject by examining the continuity equation. This time, we’ll be taking a close look at the concepts of (and relationship between) pressure and head.
What we’ll consider here is pressure in all of its forms (including vacuum) and the four measurable types of head – the energy terms and the resistance to flow. This will take us to Bernoulli’s equation, a complex mathematic construct that explains these fundamental aspects of hydraulic science.
DIGGING IN
The above is certainly a huge conceptual bite and the specific mathematics can be challenging to absorb. But there’s a reward at the end: Putting all of these concepts in order and understanding the relevance of Bernoulli’s equation is the key to seeing just why it is that faster water velocity means lower pressure and slower water velocity means higher pressure.
If we approach these important concepts systematically and figure out the relationships, we’re in a much better position to understand the systems we’re designing and installing. Let’s begin by defining some basic units used to measure pressure and head in all of their forms.
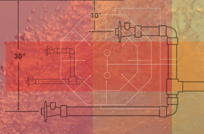
| Figure 1: The 144 one-inch-square water columns in a cubic foot of water are used to define feet of head. At sea level, one of these units weighs .433 pounds. |
A cubic foot of water is a fundamental unit used to define the basic properties of pressure and head and can be looked at in several different ways. For starters, a cubic foot of water is equal to 7.48 gallons and weighs 62.3 pounds at sea level. This cubic foot can also be segmented into 1,728 cubic inches or viewed as 144 water columns, each of them a foot tall with a one-square inch surface area (Figure 1).
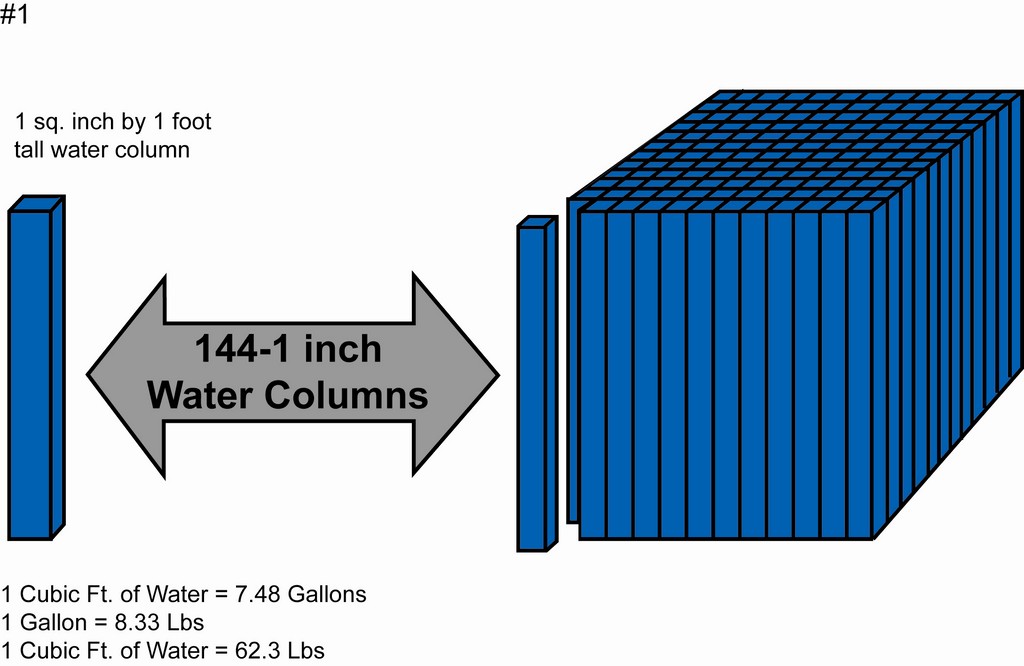
| Figure 2: Stretching the inch-square water column from 1 foot to 2.31 feet raises the weight of water in the column to 1 pound – and literally defines ‘one pound per square inch’ or ‘1 psi.’ |
These 144 water columns are used to define feet of head, that is, a one-foot-tall water column with a one-square-inch surface area is equal to one foot of head. If this one-foot-tall, one-inch-square water column were put on a scale at sea level, it would weigh .433 pounds. This tells us that this one-foot water column or one foot of head is equal to .433 pounds per square inch (psi). If we took this same one-foot water column and stretched it out to be 2.31 feet tall, it would have a weight of one pound or one psi (Figure 2).
This conversion – that is, one foot of head equals .433 psi and one psi equals 2.31 feet of head – is very important: We will use this information to convert back and forth freely from head to pressure (a trick that will be used very heavily in future articles).
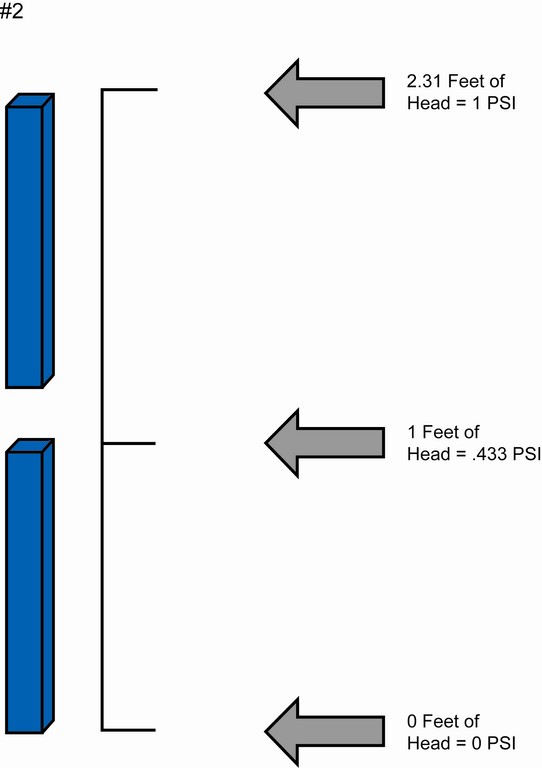
For its part, pressure can defined as a force that is perpendicular to the area of a surface. The usual place to read pressure on a swimming pool/spa system is at the filter, where the force projected by the water against the internal walls of the filter tank creates pressure that can be read using a pressure gauge (Figure 3).
| Figure 3: In a common filter tank, pressure is the perpendicular force of water pushing on the tank’s interior – a pressure that can be read using the tank’s pressure gauge. Pressure gauges read the difference between ‘internal psi absolute’ and ‘external psi atmospheric’ – which in turn equals ‘psi gauged.’ |
This type of pressure is called gauged pressure. In the pool/spa industry, we frequently refer to this gauged pressure and that’s about it, but this is not the only type of pressure we need to understand in designing custom swimming pools, spas and waterfeatures.
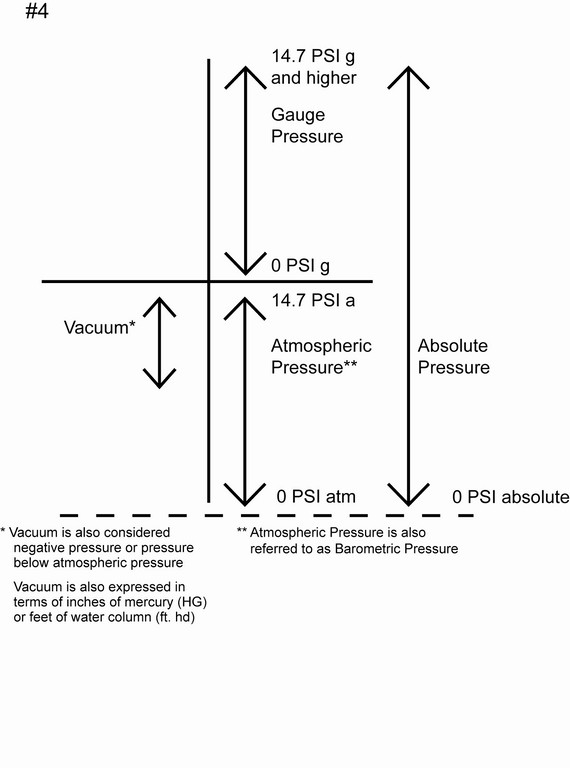
Figure 4 shows the relationships among four types of pressure. Atmospheric pressure is 14.7 psi and is the starting point for gauged pressure. When placed below gauged pressure on a chart like this, atmospheric pressure is also called barometric pressure. When you put them together, gauged pressure plus atmospheric (or barometric pressure) equals absolute pressure.
An absolute pressure equal to zero creates a condition known as a perfect vacuum and cannot be achieved only beyond Earth’s atmosphere in the vastness of space. A vacuum exists below atmospheric pressure and is normally measured in inches of Mercury (Hg) or negative gauge pressure.
| Figure 4: The relationships between the forms of pressure are seen in this chart. Vacuum is considered ‘negative pressure’ (that is, pressure below atmospheric pressure) and is expressed in terms of inches of mercury (Hg) or by water-column feet (that is, feet of head). |
A perfect vacuum checks in at 30 inches of Mercury, 33.9 feet of head or (-) 14.7 psi as gauged pressure (again, see Figure 4). Vacuum can be converted to feet of head by using a multiplier of 1.13 – another useful conversion factor.
HEAD EXAMINED
In designing a hydraulic system, the first step involved in selecting the proper pump is understanding the amount of energy or head required to move water to serve specific applications, whether it’s about moving water to a spa-jet manifold, a vanishing-edge weir or any of a number of other pool, spa or waterfeature effects.
To work in this arena, we need to pull apart the terms head and feet of head and define four common terms from fluid mechanics: velocity head, pressure head, elevation head and head loss. The first three are about energy, while the fourth is used to describe friction loss and the consequential pressure drop that occurs in piping networks.
Lets look at the first three terms and some basic hydraulic/mathematic nomenclature.
[ ] Elevation head. This is the potential energy that occurs in the water as a result of its elevation above some given point, with this difference in elevation being useful in solving basic problems in fluid mechanics. The head or energy is converted to work, for example, if the force of gravity moves the water across a vertical distance to some lower level.
In a system that has a pump, the two elevation points might be the pump’s centerline and the water’s surface. If the system is gravity-fed, however, the two points could be two vessels at different elevations that are connected by a gravity-feed line of some type. The force created by gravity is what moves water in these systems.
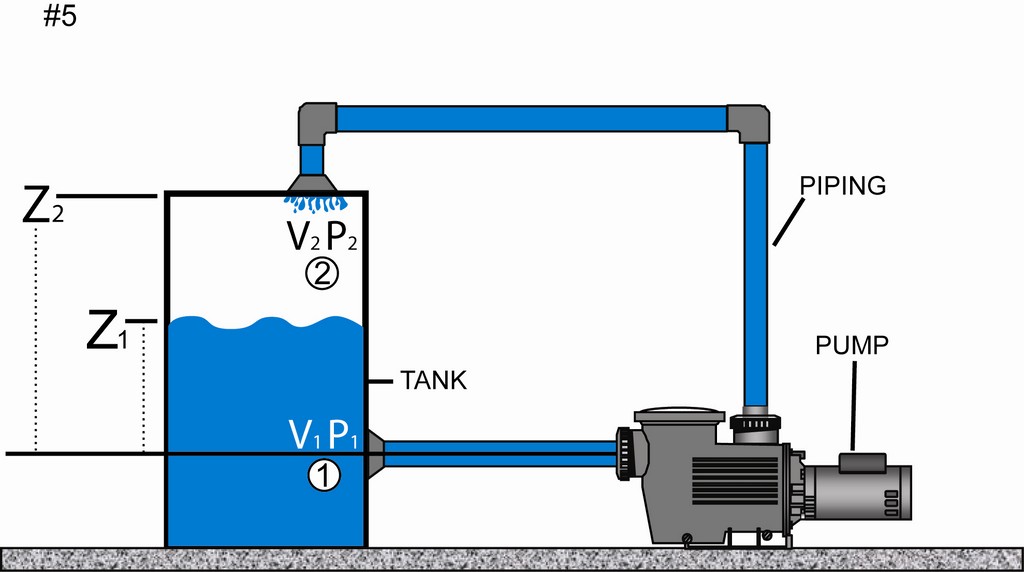
| Figure 5: Differences in elevation create pressure in hydraulic systems. Balancing the flow within these systems is about working with and balancing elevation, velocity and pressure head – and vividly defines the need for proper pipe and pump sizing. |
The difference between the two elevations is the key, and the term delta Z is commonly used to describe Z1 – Z2, that is, the difference in elevations (Figure 5). Custom swimming pools often have gravity-feed systems in their hydraulic designs. Vanishing-edge pools, for example, require backflow-prevention devices because of potential siphoning effects that occur as a result of elevation head.
[ ] Velocity head. This is the kinetic energy that occurs in the water as a result of its velocity. The faster the water travels or the higher its velocity, the greater the kinetic energy or velocity head, which is commonly expressed using the equation v2/2g (where v is velocity and g is gravity). As we learned in the last article, high velocities occur when the pipe’s flow section or size decreases – the foundation for our discussion of the continuity equation.
Applications in which high velocity is important would include spa jets or fountain nozzles – anything in which nozzle or outlet size decreases as the water flows toward the point of discharge. The velocity is at its peak just before the discharge point. This velocity head is expressed in feet per second squared over 2 gravities (with each gravity being 32.2 feet per second).
[ ] Pressure head. This is the pressure energy that represents the amount of work needed to move the water within a pipe or conduit (again, see Figure 5). Pressure head is required to overcome a pressure or vacuum in a piping network located up or downstream of a pump. Water always moves from a region of high pressure to low pressure if the pipe size or flow section remains constant, a phenomenon commonly stated as PSI (pounds per square inch) as p144/62.3.
As mentioned earlier in this article, psi or pounds per square inch is equal to 144 divided by the specific weight of water, which is 62.3 pounds per cubic foot. A one-foot water column with one square inch of surface area translates to .433 pounds. To convert psi to feet of head, we multiply psi by 2.31.
Understanding this specific relationship helps us in sizing components based on pressure and head in addition to flow – a key to proper specification of systems including spa jets, fountains and in-floor cleanings systems – just a few of the watershape systems that have both pressure and flow requirements.
Wrapping up this set of definitions, we come to head loss, which is the friction loss or pressure drop that accumulates in the piping network as a result of pipe lengths, fittings, valves and water’s passage through assorted components. (This topic will be discussed in detail in the next article, where we’ll cover both the coefficient of friction and the Darcy equation.)
DOING THE MATH
Now we come at last to Bernoulli’s equation, the mathematical construct used to explain a concept known as conservation of energy.
Basic physics tells us that energy can neither be created nor destroyed in a closed-loop system (which does not include most watershapes): It can only be transformed from one form to another. Bernoulli gave us a way of understanding the shift from one form of head to another – and offers us a key to understanding the constant shifts from velocity to head pressure we are now ready to observe and accommodate in our piping networks.
In essence, Bernoulli’s equation gives us a way of understanding the shift from one form of head to another as a result of conservation of energy. Simply put, the equation states that the total energy at any point is equal to the sum of the elevation head, the velocity head and the pressure head. If the system has no energy added to it and there are no friction losses, then the equation is Z + 144P/P + v2/2g = H.
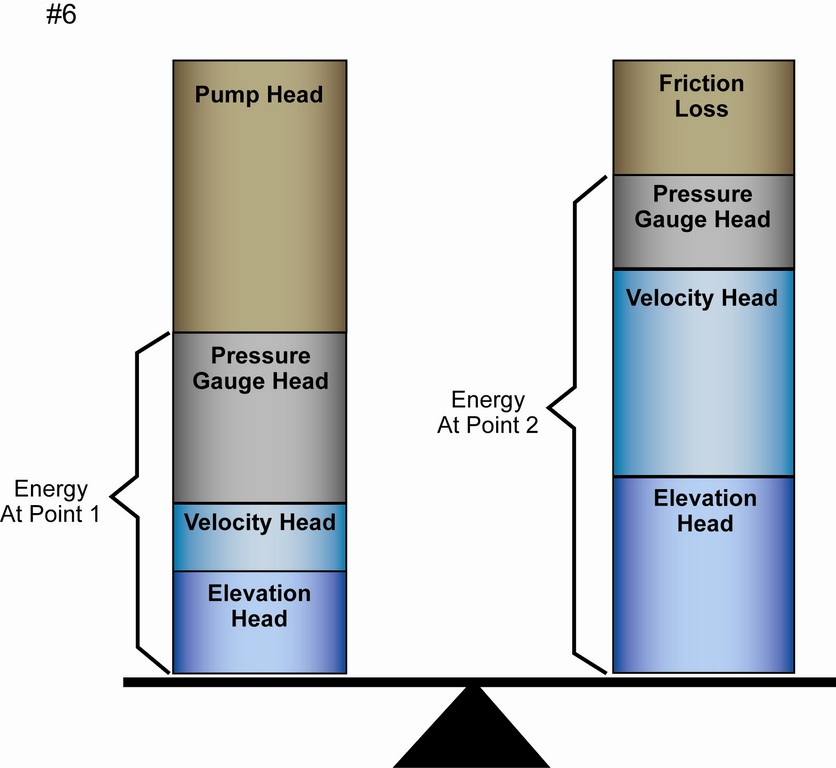
| Figure 6: Hydraulic-system design is all about balance and making certain that the pump you’ve selected will adequately overcome frictional losses and keep the other pressure factors in alignment. |
The reality, however, is that systems have increases in energy because of the use of pumps and friction losses because of piping and fittings. To accommodate those factors, the equation is rewritten as Z1 + 144 P1/P1 + v12/2g = Z2 + 144 P2/P2 + v22/2g + hL. The changes reflect the difference as the water moves from point one to point two. When the formula shows these two points, the energy balance can be observed (Figure 6).
Don’t despair: You’ll probably never, ever be called on to plug values into this equation and actually come up with an answer. What you should understand is this: Bernoulli’s equation helps explains the shift in energy that occurs in a piping system that has water pumped into it and underscores the fact that there’s always a need for balance. That is, if the velocity of the water increases, then there will be a reduction in pressure; if there’s an increase in elevation, there will be a reduction in pressure or velocity.
In other words, the sum total of the pressure head, velocity head and elevation head will never change, but the proportions among them will. When we add a pump, its head or energy is equal to the difference in elevation head, the difference in pressure head, the difference in the velocity head and the frictional loses attributable to the piping, fittings and components.
You may never need to do the math, but what you should know is that the systems you’re developing are subject to some heavy-duty rules that govern their performance. If you lack the expertise or experience needed to put everything together on your own, good system performance will only be assured if you know where to go to get answers – and then put the advice to good and purposeful use.
We’re still just part of the way into this examination of all you need to know to design effective, efficient hydraulic systems for a custom swimming pool, spa or waterfeature. A real understanding of all the factors influencing what you do extends beyond flow, head and pressure to include pressure drops – the subject of the next article in this series.
The detailed discussion this time leads to the fundamental observation that the smaller the flow section of a pipe, the faster the velocity of the water and the lower the pressure and, conversely, the larger the flow section of the pipe, the slower the velocity of the water and the greater the pressure. These are fundamental building blocks in hydraulic science – a set of relationships you should never forget.
Steve Gutai is Director of New Product Development, Hydraulics and Heating Systems, at Zodiac Pool Systems, Vista, Calif. He may be reached at [email protected].